We live in a world where numbers power everything—from your bank balance to the size of the universe. But sometimes, numbers stretch far beyond everyday use. They become so massive, they’re (almost) absurd.
Yet, they exist. And they tell us a lot about the extremes of science, math, computing, and even human curiosity.
Still, it’s important to remember: these are only the numbers we’ve managed to define. In reality, numbers go on forever. There are an infinite number of numbers, and it’s impossible to give each one a name or role.
Even the ones we do name are just tiny markers on a never-ending line.
However, we need to explore them. Some are used in cryptography. Others are part of mind-bending math discoveries. And a few exist just because someone decided to push the limits of what’s possible.
So, let’s begin.
1. The Largest Known Prime Number

Prime numbers are whole numbers greater than 1 that can only be divided evenly by 1 and themselves. They are the fundamental building blocks of the positive integers.
And as numbers grow larger, discovering new prime numbers becomes increasingly difficult, making the discovery of a massive prime a significant achievement in mathematics.
Currently, the largest known prime number is 2^136,279,841 − 1, a Mersenne prime with 41,024,320 digits. This record-breaking prime was discovered on October 12, 2024 by Luke Durant, a volunteer in the Great Internet Mersenne Prime Search (GIMPS) project, where thousands of computers worldwide collaborate to find gigantic primes.
Wait, but what is a Mersenne prime?
Well, a Mersenne prime is a special type of prime number that can be expressed in the form 2^p − 1, where p itself is prime. Not every prime exponent p produces a Mersenne prime, making each discovery rare and remarkable — especially since these primes are enormous.
So, to put the scale into perspective: if you tried reading this number aloud at a pace of 1 digit per second, it would take you over 475 days of continuous reading!
📌 Interesting fact: Printing this prime would require more than 15,000 pages, far exceeding the length of most books.
2. Googol
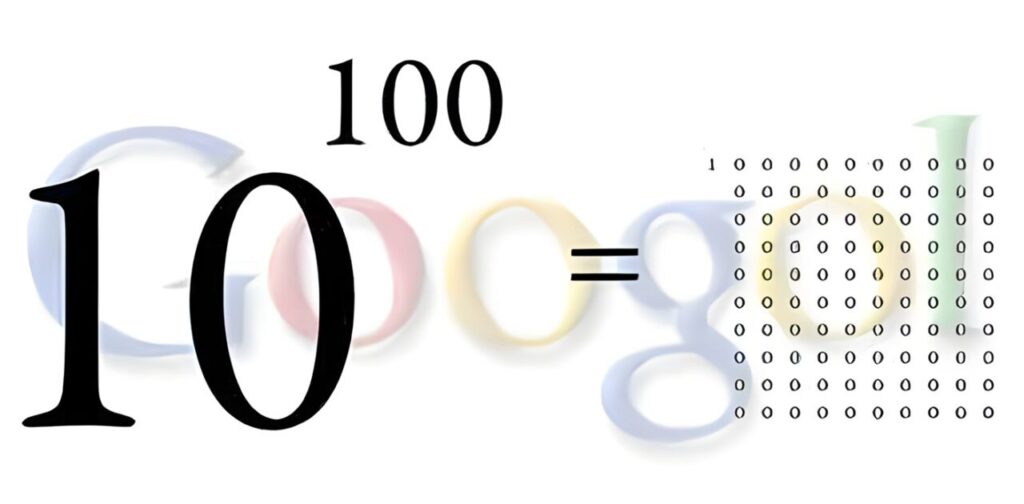
The googol is one of the most iconic large numbers, even though it’s rarely used in actual calculations. It’s a 1 followed by 100 zeros:
10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
That’s already too long to type or read in full without getting lost.
Interestingly enough, the term was coined by 9-year-old Milton Sirotta, the nephew of American mathematician Edward Kasner, in the early 20th century. The point of the googol wasn’t to use it in practice but to illustrate the difference between unimaginably large numbers and infinity.
While it’s smaller than other numbers on this list, its fame is what makes it stand out. It’s the kind of number you might think of as “so big it’s silly,” and that’s pretty much the idea.
📌 Interesting fact: A googol is far larger than the estimated number of particles in the known universe, which scientists estimate to be around 10⁸⁰.
3. Googolplex

If a googol is a giant, then a googolplex is a colossus. A googolplex is a 1 followed by a googol zeros—that is, 10 raised to the power of a googol.
Basically, this number is so big that you could never write it out fully. Not just because it would take too long—but because there isn’t enough matter in the observable universe to store all the zeros.
Even if every atom in the universe were a digit, you still couldn’t list them all. In fact, most representations of the googolplex just write “10^10^100” because there’s no other way to show it.
📌 Interesting fact: If you started writing the digits of a googolplex at a rate of one digit per Planck time (the shortest measurable unit of time), the universe would die of heat death long before you finished.
4. Graham’s Number
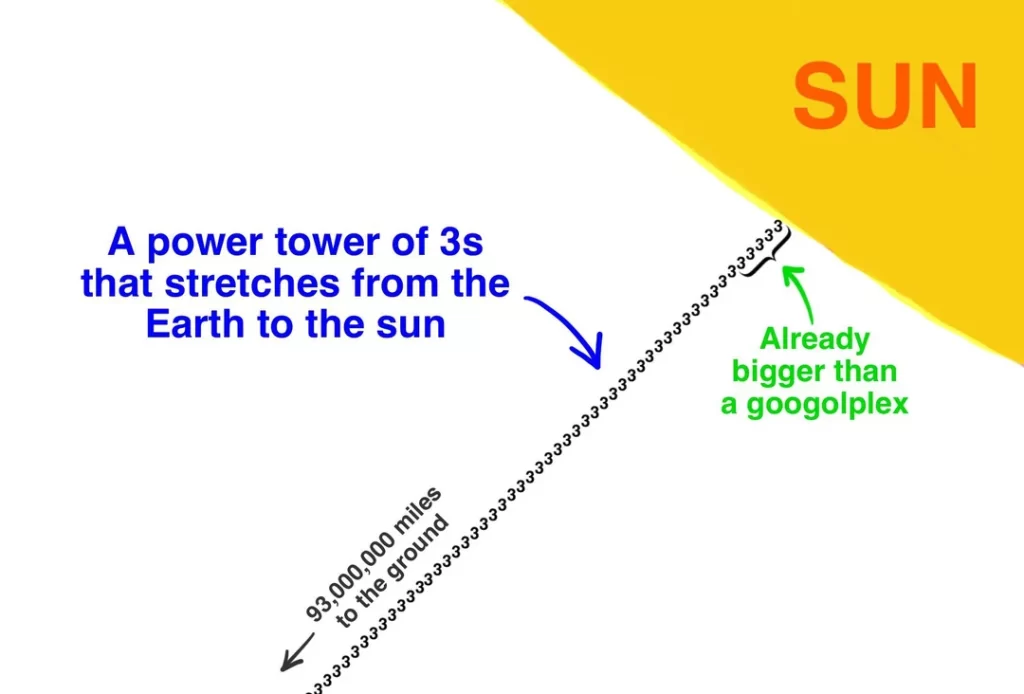
When a number is too large to write even using scientific notation, mathematicians turn to up-arrow notation, invented by Donald Knuth. That’s the only way to express Graham’s Number.
This number appeared in a problem involving connections between points in space (in Ramsey theory). Mathematician Ronald Graham used it to set an upper bound for a problem that couldn’t be solved exactly.
The number is so absurdly large that not even power towers (like 3^3^3^3) come close. Instead, it uses repeated layers of up-arrow notation. Even just the first step in building Graham’s Number already produces more digits than there are atoms in the universe.
So let’s try to explain those repeated layers of up-arrow notations:
Step 1: Define the up-arrow notation
- a↑b=ab (ordinary exponentiation)
- a↑↑b=a power tower of a’s of height b.
- More arrows represent iterated exponentiations. For example:
a↑↑↑b=a “tower” of power towers, iterated b times.
Step 2: Define the sequence used in Graham’s number:
We create a list of numbers G1,G2,…,G64, where each number grows unimaginably larger than the previous one.
- The very first number G1 is:
G1=3↑↑↑↑3
This means “3 with 4 up-arrows 3,” which is already an extremely huge number. (Four up-arrows means a super-powerful version of exponentiation repeated several times.)
- For every next number Gn (where n is 2 up to 64), we do this:
Gn=3↑Gn−13
This means: take the number Gn−1 (the previous number in the sequence), and use that many up-arrows between two 3s.
Step 3: The final Graham’s number is:
G=G64=3↑G63 3
📌 Interesting fact: Though we don’t know the entire number, we do know the last 13 digits: 7262464195387.
5. The Largest Known Perfect Number

A perfect number is a number that equals the sum of all its proper divisors. For example, 28 is perfect because 1 + 2 + 4 + 7 + 14 = 28.
These numbers are rare and mathematically beautiful. And we have a beauty right in front of us now.
Namely, the largest known perfect number, connected to the largest Mersenne prime, has about 82 million digits. It’s the result of multiplying that Mersenne prime by a very specific formula: 2^(p−1) × (2^p − 1), where p is the exponent in the Mersenne prime.
Interestingly enough, these perfect numbers have fascinated thinkers for thousands of years—from ancient Greece to the digital age. And every time we discover a new Mersenne prime, we automatically get a new perfect number.
📌 Interesting fact: Despite how big they are, all known perfect numbers are even. Nobody has ever found an odd perfect number, and it’s not clear if one even exists.
6. Avogadro’s Number

While Avogadro’s Number isn’t as long in digits as some of the others, it earns its place because of how often it’s used—and what it represents.
This number is used in chemistry to count atoms and molecules. One mole of any substance contains 6.022 x 10²³ particles.
This helps scientists connect the atomic scale (which we can’t see) to the lab scale (which we can measure). For example, 18 grams of water contains that many water molecules—602 sextillion of them.
📌 Interesting fact: If you had Avogadro’s number of marbles, you could cover the entire Earth in a layer of marbles over 80 kilometers deep.
7. Skewes’ Number

Sometimes, numbers become famous not because they’re used daily, but because they represent a turning point in understanding.
Skewes’ Number is one of those. First proposed in the 1930s, it was an estimate for when one function (the prime-counting function) surpasses another (the logarithmic integral). The number was 10^(10^10^34)—a number with so many zeros that it can’t be written or imagined easily.
Later, better methods showed that the actual crossover point is much smaller, but Skewes’ Number remains a symbol of how mathematicians sometimes overshoot before narrowing things down.
📌 Interesting fact: Skewes’ Number held the record for the largest number used in a math proof for decades.
8. Infinity

Infinity isn’t a number in the normal sense. You can’t reach it, and you can’t count to it. But it shows up everywhere—from calculus to cosmology.
It’s the concept of something that has no end. There’s no final number. And in math, there are even different sizes of infinity.
For example, there are infinite whole numbers, but there are even more real numbers between 0 and 1. That’s a strange idea, but it’s mathematically sound.
📌 Interesting fact: The infinity symbol (∞) was first used by John Wallis in 1655. Before that, there was no agreed symbol for this concept.
9. Tree(3)
Now we get into the weird zone. Tree(3) comes from a simple-sounding problem in graph theory: how many rooted trees can you create under certain rules?
The answer: Tree(3). That’s the name of the number—and it’s the largest finite number ever used in a published mathematical proof.
It’s so massive that we don’t know its size, can’t calculate it, and can’t meaningfully compare it to other numbers. But we know it’s finite. That’s both comforting and terrifying.
📌 Interesting fact: You can’t even reach Tree(3) by stacking up Graham’s Numbers. It’s bigger than anything else on this list. (except something at the end, outside the list.)
10. The Longest Decimal Expansion of Pi Computed (105 Trillion Digits)

Pi (π) is the ratio of a circle’s circumference to its diameter. It’s an irrational number, which means it goes on forever without repeating.
In 2022, a team used advanced computing to calculate 105 trillion digits of pi. That’s over 105,000,000,000,000 digits after the decimal point.
These calculations aren’t just about vanity. They test computer speed, memory handling, and software precision. They’re benchmarks for cutting-edge computing.
📌 Interesting fact: Even with all these digits, only the first 40 digits of pi are ever used in scientific calculations. The rest are just… extra.
So, What Is the Biggest Number in the Universe?

Well, this is not an easy question to answer. Namely, we did provide top 10 biggest numbers, by using somehow “normal” mathematics.
However, when exploring incredibly large numbers, things become somewhat abnormal. Namely, mathematicians have discovered finite numbers so big (large, huge, enormous, whatever…) that they defy ordinary comprehension.
And one of the largest known among these is called SSCG(3). Yes, something like from pure sci-fi .
Why SSCG(3)?
SSCG(3) stands for the “Simple Subcubic Graph function at 3,” and it comes from a highly specialized branch of combinatorics involving graphs and how they can be embedded and arranged.
This number is part of a fast-growing hierarchy of functions designed to measure incredibly complex mathematical structures.
SSCG(3) is so mind-bogglingly large that it outstrips even the famously huge TREE(3) by an almost unimaginable margin. In fact, SSCG(3) grows faster than any finite number you can build by repeatedly applying TREE functions or similar constructions.
It’s a finite number with a precise mathematical definition, but too enormous to write out or meaningfully express using any conventional or even exotic notation. Like TREE(3), it’s known to be finite and rigorously defined but completely beyond any normal scale.
So…Why Does it Matter?
Numbers like SSCG(3) push the boundaries of what we can conceive about size and complexity in mathematics. While googolplex and Graham’s number capture popular imagination for their size, SSCG(3) belongs to an elite class of numbers that go far far beyond.
📌 Interesting fact: Even though SSCG(3) is larger than almost anything you can imagine, its existence is proven, and it plays a role in understanding deep structural questions in mathematics.
How many digits does SSCG(3) have?
- We cannot meaningfully state how many digits SSCG(3) has. The number SSCG(3) is so enormous that it far exceeds not only powers of 10 but also any conventional or extended notation we have, including Knuth’s up-arrow or even TREE-based hierarchies.
- Unlike “normal” large numbers (like the largest known prime or perfect number) whose digits can be counted or approximated, SSCG(3) is beyond such expression.
- It does not make sense to talk about its decimal expansion length, since SSCG(3) is unimaginably larger than any tower of exponents whose height you can conceive.
- Even TREE(3), which is smaller, is too big to express digits for.
Hence, SSCG(3) has more digits than any physically realizable notation can describe; it is inconceivably larger than anything you know like prime digit counts, googolplex digits, or Graham’s number scale.
Is there any number bigger than SSCG(3)?
- Currently, SSCG(3) is the largest finite number with a commonly agreed-upon name and precise mathematical definition used in research (specifically in combinatorics on graphs). However, numbers like Rayo’s number and Loader’s number are also somewhere there at the top and it is not easy to compare them.
- Mathematicians can always define larger numbers by inventing new fast-growing functions or hierarchy extensions, but in terms of named finite numbers known and studied today, SSCG(3) is the biggest standing record.
- Beyond SSCG(3), you enter the realm of arbitrarily defined or constructed fast-growing functions without standard names.
- Infinity is not a number, but a concept representing unbounded size, so it is “larger” but fundamentally different.
To answer this in one sentence: there is NO biggest number because the set of natural numbers is infinite.
Summary Table of Largest Numbers
| Number | Size / Digit Count (if known) | Notable Comparison / Fact |
|---|---|---|
| Largest known prime | 2^136,279,841 − 1 (41,024,320 digits) | Discovered Oct 12, 2024 by Luke Durant. Would take 475+ days to read aloud. Requires 15,000+ pages to print. |
| Largest known perfect number | About 82 million digits | Created from largest known Mersenne prime. All known perfect numbers are even. |
| Googol | 10^100 (1 with 100 zeros) (101 digits) | Coined by 9-year-old Milton Sirotta. Much larger than the number of particles in the universe (~10^80). |
| Googolplex | 10^(10^100); 1 with a googol zeros (101 digits in exponent) | So big, can’t write it out. More zeros than there are atoms in the universe. |
| Graham’s number | Not expressible in digits | Last 13 digits are 7262464195387. Far exceeds googolplex. Defined by up-arrow notation. |
| Avogadro’s Number | 6.022×10^23 | Number of atoms/molecules per mole. Enough marbles to cover Earth with 80km layer. |
| Skewes’ number | 10^(10^10^34) | First really huge number used in proof. Later improved but symbolically remains famous. |
| Infinity | Not a finite number | Infinite sizes—there are even “more” real numbers than whole numbers. Symbol ∞ first used in 1655. |
| TREE(3) | Not expressible in digits | Largest finite number in a published mathematical proof. Far bigger than Graham’s number. |
| Pi decimal expansion (2022 record) | 105 trillion digits (105,000,000,000,000) | Only first 40 digits needed for any calculation. Computed as benchmark for computers. |
| SSCG(3) | Not expressible, unimaginably larger than any above | Largest finite named number used in math. Digit count cannot be meaningfully stated—beyond all notations. |