Mathematics is an extremely interesting field, even though our schooling system often leads many of us to develop a big dislike for math from an early age.
We were taught that we needed to solve various equations without understanding why. What’s the purpose behind all of that?
Well, the main reason (and often the only one), was to get a relatively good grade.
That’s it.
However, mathematics with its complex equations and formulas have the power to solve some of the world’s biggest problems and mysteries.
Many math equations really moved the world forward.
However, there are still some equations or math problems that even the brightest minds in the field have not been able to solve.
These unsolved equations are completely and utterly non-understandable for 99,999% of the population.
Heck, even many great mathematicians struggle to understand them.
Yet, those problems or equations do exist in one form or another.
And so, in this article, we will be discussing the top 5 math equations that are yet to be solved or perhaps completely dismissed.
These equations have been studied and analyzed by mathematicians for many years, but no one has been able to find a solution.
And so, let’s begin with this rather complex list.
First, we’ll try to explain the equations and math problems as they are (very complex), and then we’ll explain them in a more simple way – the ELI5 way (Explain Like I’m Five), if that’s even possible.
Let’s see…
Interesting fact: Did you know that the number 0 is an even number? This might seem trivial, but it's interesting because it challenges some common misconceptions about even and odd numbers. By definition, an even number is any integer that is divisible by 2 without leaving a remainder. Since 0 divided by 2 equals 0 with no remainder, it fits this definition perfectly, making it an even number.
1. Riemann Hypothesis
The Riemann Hypothesis is one of the most famous and important unsolved problems in mathematics.
It was first proposed by Bernhard Riemann in 1859 and remains unsolved to this day.
The hypothesis is concerned with the distribution of prime numbers, which are the building blocks of all natural numbers.
Zeta Function
The Riemann Hypothesis is intimately connected to the zeta function, which is a mathematical function that is used to study the distribution of prime numbers.
The zeta function is defined for all complex numbers except for the number 1.
The hypothesis states that all non-trivial zeros of the zeta function lie on the critical line of 1/2.
This means that if the hypothesis is true, then the distribution of prime numbers can be predicted with a high degree of accuracy.
Zeta function looks like this:
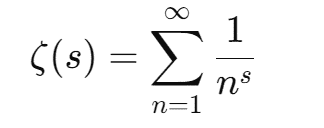
Prime Number Distribution
The Riemann Hypothesis also has big implications for the distribution of prime numbers.
If the hypothesis is true, then it would provide a formula for calculating the number of primes less than any given number.
This would have significant implications for cryptography, which relies on the difficulty of factoring large numbers into their prime factors.
Riemann Hypothesis – ELI5

Okay, now for the tough part… Let’s try to explain this in simpler terms.
Let’s imagine you have a magical machine called the Riemann zeta function. This machine does some delicate math stuff with numbers.
Now, imagine you’re looking for special points on a map.
The Riemann Hypothesis is like a big guess saying, “Hey, all the really important points on this map are located in a certain way.“
Imagine you have a specific type of number, kind of like a secret code, called a “complex number.”
The Riemann Hypothesis says that if you plug in one of these special numbers into the Riemann zeta function (machine), you’ll always get a particular answer: zero.
It’s like finding the most important spots on the map – they’re always in the same place.
So, the equation for the Riemann Hypothesis is just a fancy way of saying, “When you use this special machine and put in these special numbers, the answer you get is always zero.”
It’s a bit like a treasure hunt in math, trying to find where all these special spots are hidden, which could help us understand a lot more about numbers overall.
2. Navier-Stokes Existence and Smoothness
Fluid Dynamics
The Navier-Stokes equations are a set of partial differential equations that describe the motion of fluids.
They are commonly used in engineering and science to model everything from the flow of air over an airplane wing to the behavior of blood in the human body.
Despite their importance, mathematicians have yet to prove the existence and smoothness of solutions to the Navier-Stokes equations in three dimensions.
One of the challenges in solving the Navier-Stokes equations is that they are highly nonlinear, meaning that small changes in the initial conditions can lead to very different outcomes.
This makes it difficult to predict the behavior of fluids in complex systems. Another challenge is that the equations involve both velocity and pressure, which are coupled together in a way that is not fully understood.
The Navier-Stokes problem can be written as:
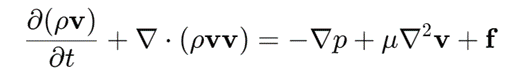
Fancy, huh?
Millennium Prize Problem
The Navier-Stokes existence and smoothness problem is one of the seven Millennium Prize Problems, a set of unsolved mathematical problems that were identified by the Clay Mathematics Institute in 2000.
The institute offered a prize of one million dollars for the solution to each problem.
However, no one yet received the money for Navier-Stokes Existence and Smoothness.
Not that people haven’t tried.
They did, very hard however no success yet.
Navier-Stokes Existence and Smoothness – ELI5

So, imagine you’re watching a river flow. The Navier-Stokes equations are like a super-detailed instruction manual that tells us how the water moves and behaves.
The “existence” question is asking whether this instruction manual always works, regardless of what the river looks like at the start.
It’s like wondering, “Can we always trust this manual to tell us how the river flows, no matter what?”
Now, the “smoothness” question is asking if the river’s behavior stays nice and smooth, like a gentle stream, or if it can suddenly turn chaotic, with wild currents and turbulence.
We’re trying to figure out if the manual always keeps things calm and predictable or if it allows for some crazy surprises.
So, in simpler terms, mathematicians are still trying to understand if the manual for how rivers flow always works perfectly and if it keeps the river’s behavior nice and smooth, or if it sometimes lets things get really hectic.
It’s a rather tough problem, but mathematicians are still working hard trying to solve it!
3. P vs NP Problem

Computational Complexity
The P vs NP problem is one of the most famous and yet unsolved problems in computer science.
The problem is to determine whether every problem that can be solved by a non-deterministic polynomial time (NP) algorithm can also be solved by a deterministic polynomial time (P) algorithm.
The importance of this problem lies in its implications for computational complexity theory.
If P = NP, it would mean that many problems that are currently considered to be intractable can be solved efficiently.
This would have enormous implications for fields such as cryptography, optimization, and artificial intelligence.
The problem is also listed as one of the seven Millennium Prize Problems by the Clay Mathematics Institute, with a prize of $1 million offered for its solution.
P vs NP Problem – ELI5

Imagine you’re packing for a trip. Some items are easy to fit into your suitcase (P), and you can quickly tell if they’ll fit or not.
Other items are a bit trickier—they might fit, but you have to try lots of different arrangements to be sure (NP).
Now, here’s the twist: What if there’s a special bag that, no matter how big or awkwardly shaped the item is, you can always find a way to pack it quickly and easily?
That’s what the P vs NP problem asks: “Is there a magical packing method that can turn any tricky item into an easy-to-pack one?”
If such a method exists, it would change the game for all sorts of packing challenges (or, in computing terms, problem-solving tasks).
But for now, it’s still an unsolved problem waiting for someone to discover the ultimate packing hack!
4. Birch and Swinnerton-Dyer Conjecture

The Birch and Swinnerton-Dyer Conjecture is certainly one of the top 5 unsolved problems in mathematics.
It concerns elliptic curves, which are a fundamental object of study in number theory.
The conjecture was first proposed in 1960 by Bryan Birch and Peter Swinnerton-Dyer, and it remains unsolved to this day.
P.S. – Conjecture refers to the mathematical statement which appears to be true but has not been formally proven.
Elliptic Curves
An elliptic curve is a type of algebraic curve that can be defined by an equation of the form y^2 = x^3 + ax + b, where a and b are constants.
These curves have a rich structure and are of great interest in number theory, as they are intimately connected with the theory of rational points on curves.
Rational Points
The Birch and Swinnerton-Dyer Conjecture concerns the number of rational points on an elliptic curve.
A point on an elliptic curve is said to be rational if its coordinates are rational numbers.
The conjecture asserts that there is a deep connection between the number of rational points on an elliptic curve and the behavior of a certain function associated with the curve, known as its L-function.
Despite much progress in the study of elliptic curves and related objects, the Birch and Swinnerton-Dyer Conjecture remains one of the most challenging problems in mathematics.
It has been verified for a large number of elliptic curves, but a general proof has yet to be found.
Birch and Swinnerton-Dyer Conjecture – ELI5

The Swinnerton-Dyer Conjecture is like a really tricky puzzle in math, and imagine someone just cracked it!
So, this puzzle involves something called elliptic curves. Elliptic curves are wavy lines on a graph that have a special property: if you draw a straight line through them, it will hit the curve in at most three places.
They’re like math’s Swiss Army knife, used in lots of different fields because they’re really good at solving all sorts of problems!Top of Form
Now, the Swinnerton-Dyer Conjecture is all about understanding these curves better, especially how many points they have.
So, when someone says they solved the Swinnerton-Dyer Conjecture, it’s like saying they found the missing piece to complete a giant jigsaw puzzle.
It’s a really big deal in the math world because it helps us understand these special shapes called elliptic curves a whole lot better.
5. Hodge Conjecture

The Hodge Conjecture is one of the most challenging problems in mathematics.
It is a statement about the relationship between algebraic cycles and differential forms on complex algebraic varieties.
The conjecture was first proposed by William Hodge in 1950 and has been an open problem ever since.
Algebraic Cycles
The Hodge Conjecture asserts that every Hodge class on a complex algebraic variety is a linear combination of classes of algebraic cycles.
An algebraic cycle is a formal linear combination of subvarieties of the variety, with integer coefficients.
The Hodge Conjecture implies that every Hodge class can be represented by an algebraic cycle.
Differential Forms
Differential forms are a fundamental concept in differential geometry and topology.
They are used to study the geometry of manifolds and to define important invariants such as the De Rham cohomology.
The Hodge Conjecture states that every Hodge class can be represented by a differential form.
The Hodge Conjecture has been partially solved in some special cases, but a general proof is still missing.
The conjecture is closely related to other important problems in algebraic geometry and topology, such as the Birch and Swinnerton-Dyer Conjecture and the Mumford-Tate Conjecture.
Hodge Conjecture – ELI5
Imagine you have a weird shape, like a blob or a twisted doughnut. Mathematicians love studying shapes like these, especially when they’re in a higher dimension than what we can easily visualize.
Now, imagine drawing lines on this shape. These lines could be paths that wind around the shape in different ways.
Some paths might be simple, like going straight across, while others might twist and turn.
The Hodge Conjecture is all about understanding these lines or paths on the shape and how they behave.
It says that certain types of paths, called algebraic cycles, can be built by adding up simpler paths in a smart way.
Why is this important?
Well, it helps mathematicians understand the structure of these shapes in really deep ways. It connects different areas of mathematics and sheds light on some of the deepest mysteries of geometry and algebra.
But here’s the kicker: while the Hodge Conjecture is widely believed to be true, it’s still a conjecture, which means it hasn’t been proven yet completely.
Conclusion

There are hundreds of unresolved mathematical problems out there. Some will be solved probably in a matter of years, some will remain unsolved, and probably a good percentage will be completely dismissed.
In this article, we’ve wanted to provide a relatively easy view into the most famous unsolved mathematical problems.
And there is no easy way to explain all of those problems.
They are very complex and hard to understand so we provided the ELI5 version also.
However, ELI5 sometimes sounds even weirder than the original hypothesis.
Regardless, mathematics is probably the most important branch of science alongside physics.
Without it, many things we take for granted today wouldn’t exist, and without mathematics, we would probably still live much like in the Stone Age.
In the coming years, with the development of technology and artificial intelligence, some mathematical problems will become solvable within a few minutes.
Add to that quantum computing, and we can be sure that all the mathematical problems on our list will be solved very quickly.
Let’s just hope that all this will contribute to the progress of the world and not some dystopian regression.